
Сколько у вас день рождения в один день? В течение многих лет я не знал никого, у кого день рождения совпадает со мной, но по мере расширения круга моих знакомых росла и вероятность того, что по крайней мере у некоторых из них будет одна и та же дата рождения. Теперь я знаю как минимум еще пятерых людей с таким же летним днем рождения, как у меня. Каковы шансы?
Как работает парадокс дня рождения?
Ответ кроется впарадоксе дня рождения: Насколько большой должна быть случайная группа людей, чтобы с вероятностью 50% по крайней мере двое из них поделиться днем рождения?
Возьмем, к примеру, класс школьников. Допустим, в классе 30 детей, у которых 365 возможных дат рождения в календарном году. Вероятность того, что кто-то из студентов совпал с днем рождения, кажется довольно низкой, верно? В конце концов, в группе всего из 30 детей, чьи рождения были случайным образом распределены в 10 раз по большему количеству дней в году, ни у кого, вероятно, не будет одинаковой даты рождения, верно?
Итак, насколько большой должна быть группа случайных людей, чтобы двое из них совпали день рождения? Большинство людей, которые быстро посчитают в уме, поверят, что 182 - это правильный ответ, что составляет примерно половину количества дней в году. Но вам действительно нужно 182 человека в группе, чтобы двое из них имели одинаковую дату рождения?
Нет, все не так просто: парадокс дня рождения имеет дело с экспонентами.
Вероятность парадокса дня рождения экспоненциальна
" Самое главное, люди значительно недооценивают, насколько быстро вероятность увеличивается с размером группы. Количество возможных пар увеличивается экспоненциально с размером группы. И люди ужасны, когда дело доходит до понимания экспоненциального роста", Джим Фрост, статистик и обозреватель Статистического дайджеста Американского общества качества, рассказал Live Science.
Мы просто не очень хороши в угадывании вероятностей, особенно когда они так нелогичны, как парадокс дня рождения.
«Мне нравятся такие типы задач, потому что они иллюстрируют, как люди, как правило, плохо разбираются в вероятностях, заставляя их принимать неверные решения или делать неверные выводы», - сказал Фрост.
Чтобы понять вероятное количество людей, при котором двое из них будут близнецами, мы должны сделать математику - и начать процесс исключения.
Например, для группы из двух человек вероятность того, что у одного человека день рождения совпадает с днем рождения другого, составляет 364 дня из 365. Это вероятность около 0,27 процента. Добавьте в группу третьего человека, и вероятность того, что у вас будет общий день рождения, возрастет до 363 из 365 дней, что составляет примерно 0,82 процента.
Ответ на парадокс дня рождения
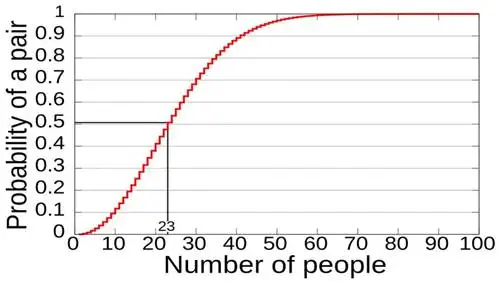
Как вы уже догадались - и правильно сделали - чем больше группа, тем выше вероятность того, что два человека родились в один и тот же день. Итак, каков правильный ответ на парадокс дня рождения? Если мы продолжим заниматься математикой, то обнаружим, что когда мы достигнем группы из 23 человек, вероятность того, что у двоих из них день рождения совпадет, составляет около 50%.
Почему 23 кажется таким нелогичным ответом? Все дело в экспонентах. Наш мозг, как правило, не вычисляет силу умножения экспонент, когда мы делаем математику в уме. Мы склонны думать, что вычисление вероятностей - это линейное упражнение, которое очень далеко от истины.
В комнате с 22 другими людьми, если вы сравните свой день рождения с днями рождения других 22 человек, получится только 22 сравнения.
Но если сравнить все 23 дня рождения друг с другом, получится гораздо больше, чем 22 сравнения. На сколько больше? Ну, у одного человека есть 22 сравнения, но второго человека уже сравнили с первым человеком, так что у этого человека есть только 21 сравнение. Тогда у третьего человека будет 20 сравнений, у четвертого - 19 и так далее. Если сложить все возможные сравнения, то всего получится 253 сравнения или комбинации сравнений. Таким образом, группа из 23 человек включает 253 комбинации сравнения, или 253 шанса совпадения двух дней рождения.
Вот еще одна проблема экспоненциального роста, похожая на парадокс дня рождения. «В обмен на какую-то услугу, предположим, вам предлагают заплатить 1 цент в первый день, 2 цента во второй день, 4 цента в третий, 8 центов, 16 центов и так далее в течение 30 дней». - сказал Фрост. «Хорошая ли это сделка? Большинство людей думают, что это плохая сделка, но благодаря экспоненциальному росту у вас будет в общей сложности 10,7 миллиона долларов на 30-й день».
Математические вероятностные вопросы, подобные этим, «показывают, насколько полезной может быть математика для улучшения нашей жизни», - сказал Фрост. «Итак, противоречивые результаты этих задач забавны, но они также служат цели».
В следующий раз, когда вы будете частью группы из 23 человек, вы можете быть уверены, что у вас есть 50-процентный шанс разделить день рождения с кем-то.
Интересно
С психологической точки зрения есть две «системы», которые мозг использует для решения проблем и принятия решений: первая система основана на интуиции и позволяет нам принимать быстрые решения, в то время как вторая система требует преднамеренного (а иногда и нарисованного) out) думая придумать ответ. Парадокс дня рождения основан на том, что вторая система вычисляет и дает правильный ответ.
Часто задаваемые вопросы
Есть ли шанс 50, что двое из них родятся в один день?
Да, с вероятностью 50% у двоих из них день рождения совпадает.
