Часто определение уравнений линий на графике может потребовать много вычислений. Но с простыми прямыми линиями практически не требуются вычисления. Вы можете просто сказать уравнение почти сразу, посчитав маленькие квадратики на миллиметровой бумаге.
Шаги
Часть 1 из 3: выяснение уравнения
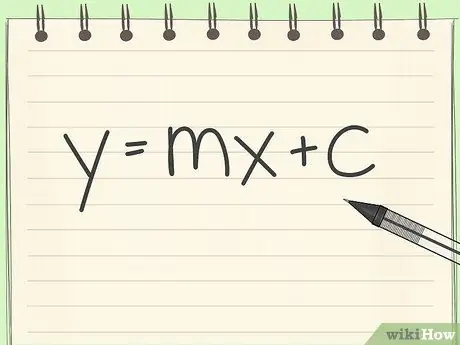
Шаг 1. Знать базовую структуру уравнений прямой
Здесь обычно будет использоваться форма пересечения наклона. Это y = mx + c, где:
- y - число по оси y;
- m - уклон или наклон линии;
- x - число по оси x;
- и c - точка пересечения по оси y.
- Чтобы избежать путаницы, помните, что y всегда должен быть положительным.
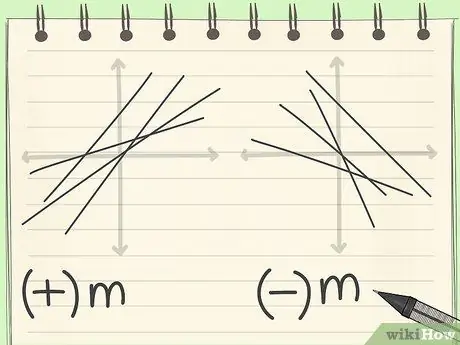
Шаг 2. Определите, отрицательны ли градиент или m
Итак, есть две стороны на выбор: y = mx + c или y = -mx + c. Если линия идет сверху справа вниз слева, m положительно. Но если линия идет сверху слева направо снизу, m отрицательно.
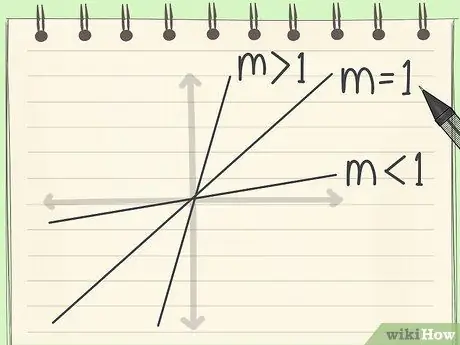
Шаг 3. Найдите градиент
Прежде чем сдаться и прибегнуть к расчету с помощью чисел, попробуйте этот более простой способ. Посмотрите, круче ли линия y = x или y = -x. Если круче, значит m> 1. Если линия более пологая или менее крутая, это означает, что m <1.
- Время считать коробки. Если m> 1, подсчитайте вертикальные прямоугольники для ширины одного горизонтального прямоугольника. Подсчитайте количество ящиков, которое требуется линии, чтобы дойти от одной точки с двойным целым числом (например, (2, 3) или (5, 1); не (5.4, 3) или (1.2, 3.9)) до другой точки с двойным целым числом.. Количество подсчитанных ящиков прямо равно m.
- Но если m <1, посчитайте горизонтальные блоки для ширины одного вертикального блока. Пусть количество посчитанных ящиков равно n. Градиент, если m <1, будет один над n или 1 / n.
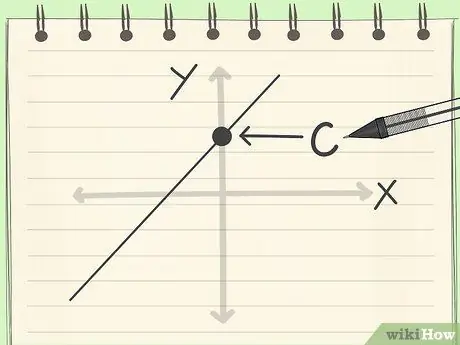
Шаг 4. Найдите точку пересечения по оси Y или c
Это, вероятно, самый простой шаг из всех, описанных в этой статье с практическими рекомендациями. Y-пересечение - это точка, в которой линия пересекает ось Y.
Часть 2 из 3: Быстрый поиск уравнения для вертикальных или горизонтальных линий

Шаг 1. Быстро взгляните на число на оси x или y
Если линия вертикальная, посмотрите на точку пересечения по оси x. Если линия горизонтальная, посмотрите на точку пересечения по оси Y. Уравнение для этих типов линий отличается от структуры y = mx + c.
- Пример 1: линия представляет собой вертикальную линию. Таким образом, мы должны посмотреть на точку пересечения по оси x. Посмотрев на него ясно, мы увидели цифру «6». Уравнение для этой линии x = 6. Это означает, что x всегда будет 6, поскольку линия прямая, поэтому она останется на 6 и не пересечет никакую другую ось.
- Пример 2: линия представляет собой горизонтальную линию. Мы должны посмотреть на точку пересечения по оси y. Уравнение y = 1, потому что горизонтальная линия останется неизменной навсегда, не пересекая ось x.
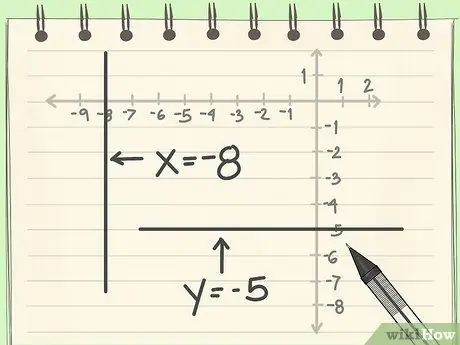
Шаг 2. Не забывайте, что линии тоже могут быть отрицательными
- Пример 3: Эта линия представляет собой вертикальную линию. Мы должны смотреть на ось абсцисс. Строка идет с числом «-8». Таким образом, уравнение для этой линии x = -8.
- Пример 4: Эта линия горизонтальная. Посмотрите на ось Y. Горизонтальная линия совпадает с цифрой «-5». Уравнение y = -5.
Часть 3 из 3: Использование примеров для отработки более сложных линий
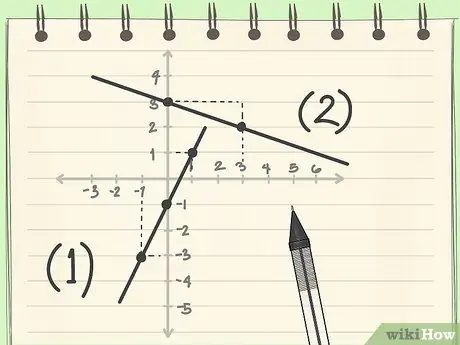
Шаг 1. Попрактикуйтесь с некоторыми базовыми невертикальными и негоризонтальными примерами
Время для чего-то более сложного!
- Пример 1. Обратите внимание, как требуется два вертикальных блока, чтобы перейти от одной точки с двойным целым числом к другой. Также обратите внимание, что он круче, чем простой y = x. Мы можем сделать вывод, что градиент равен «2». Итак, теперь у нас есть y = 2 x. Но мы еще не закончили. Нам все еще нужно найти точку пересечения по оси Y. Обратите внимание, что линия пересекает ось y в точке «-1» на оси y. Уравнение для этой линии действительно y = 2 x -1.
- Пример 2: Посмотрите, что линия идет сверху слева направо вниз, это означает, что у нее отрицательный градиент. Чтобы перейти от одной точки с двойным целым числом к другой, количество горизонтальных блоков равно 3, а количество вертикальных блоков - 1. Это означает, что градиент равен «-1/3». Пересечение оси y положительно 3, поскольку вы видите линию, пересекающую ось y. Эта линия имеет вид y = -1 / 3 x +3.

Шаг 2. Продвигайтесь к более сложным линиям
Изучите этот образ. Возможно, вы заметили это правило раньше, но изучите его, чтобы лучше узнать его. Вы также можете вернуться к некоторым прошлым примерам.
- Пример 1: Это незнакомая строка. Но посмотрите на приведенное выше правило и попробуйте применить те же рассуждения к этой строке. Эта линия имеет положительный градиент. Чтобы перейти от одной точки с двойным целым числом к другой, она поднимается на 4 блока по вертикали и на 3 блока вправо по горизонтали. Оглядываясь на приведенное выше правило, мы можем определить, что эта линия имеет градиент «4/3». Y-точка пересечения равна 2, поэтому прямая y = 4/3 x +2.
- Пример 2: Для этой строки мы могли видеть, что точка пересечения по оси Y равна «0», поэтому нам не нужно ничего добавлять для c. Имеет отрицательный градиент. Чтобы перейти от одной точки с двойным целым числом к другой, необходимо количество вертикальных блоков 3, а количество необходимых горизонтальных блоков - 4. Таким образом, уравнение y = -3 / 4 x.
