
Есть ли волшебное уравнение Вселенной? Вероятно, нет, но есть некоторые довольно распространенные, которые мы снова и снова находим в мире природы. Возьмем, к примеру,последовательность Фибоначчи Это последовательность постоянно возрастающих чисел, в которой каждое число (число Фибоначчи) является суммой двух предыдущих чисел. (Подробнее о математическом уравнении через минуту.)
Последовательность Фибоначчи работает и в природе как соответствующее соотношение, отражающее различные закономерности в природе - вспомните почти идеальную спираль раковины наутилуса и устрашающий водоворот урагана.
Люди, вероятно, знали о последовательности Фибоначчи на протяжении тысячелетий - математические идеи, связанные с этой интересной закономерностью, восходят к древним санскритским текстам между 600 и 800 годами до нашей эры. Н. Э. Но в наше время мы связываем это со всем, от одержимости одного средневекового человека кроликами до информатики и семян подсолнуха.
Числа Фибоначчи и как размножаются кролики

В 1202 году итальянский математик Леонардо Пизано (также известный как Леонардо Фибоначчи, что означает «сын Боначчи») задался вопросом, сколько кроликов может произвести одна группа родителей. В частности, Фибоначчи поставил вопрос: сколько пар кроликов может произвести одна пара кроликов за один год? Этот мысленный эксперимент показывает, что самки кроликов всегда рождают пары, и каждая пара состоит из одного самца и одной самки.
Подумайте об этом: двух новорожденных кроликов помещают в закрытую зону, где кролики начинают размножаться, как кролики. Кролики не могут рожать детенышей, пока им не исполнится хотя бы 1 месяц, поэтому на первый месяц остается только одна пара. В конце второго месяца самка рождает новую пару, в результате чего остается две пары.
Когда наступает третий месяц, первоначальная пара кроликов производит еще одну пару новорожденных, в то время как их более раннее потомство становится взрослым. В результате остаются три пары кроликов, две из которых рожают еще две пары в следующем месяце, всего пять пар кроликов.
Итак, через год сколько будет кроликов? Вот тогда и приходит на помощь математическое уравнение. Оно довольно простое, несмотря на то, что звучит сложно.
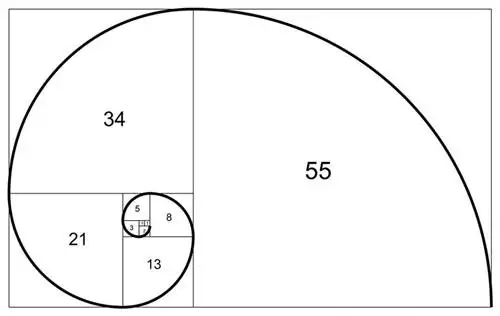
Первые числа Фибоначчи идут следующим образом: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и так далее до бесконечности.
Математическое уравнение, описывающее это, выглядит так:
Xn+2=Xn+1 + Xn
По сути, каждое целое число представляет собой сумму двух предыдущих чисел. (Вы можете применить эту концепцию к отрицательным целым числам, но здесь мы рассмотрим только положительные целые числа.)
- Чтобы найти 2, сложите два числа перед ним (1+1)
- Чтобы получить 3, сложите два числа перед ним (1+2)
Этот набор бесконечных сумм известен как ряд Фибоначчи или последовательность Фибоначчи. Соотношение между числами в последовательности Фибоначчи (1,6180339887498948482) часто называют золотым сечением или золотым числом. Отношения последовательных чисел Фибоначчи приближаются к золотому сечению по мере того, как числа приближаются к бесконечности.
Хотите увидеть, как эти удивительные числа выражаются в природе? Нет необходимости посещать местный зоомагазин; все, что вам нужно сделать, это оглядеться вокруг.
Как работает последовательность Фибоначчи в природе

Хотя некоторые семена растений, лепестки и ветки и т. д. следуют последовательности Фибоначчи, это, конечно, не отражает того, как все происходит в естественном мире. И только потому, что ряд чисел может быть применен к поразительному разнообразию объектов, это не обязательно подразумевает наличие какой-либо корреляции между числами и реальностью.
Как и в случае с нумерологическими суевериями, такими как известные люди, умирающие группами по три человека, иногда совпадение - это просто совпадение.
Но хотя некоторые утверждают, что распространенность последовательных чисел Фибоначчи в природе преувеличена, они появляются достаточно часто, чтобы доказать, что они отражают некоторые естественные закономерности. Обычно их можно заметить, изучая способ роста различных растений. Вот несколько примеров:
Семенные головки, сосновые шишки, фрукты и овощи
Посмотрите на множество семян в центре подсолнуха, и вы заметите, что они выглядят как золотой спиральный узор. Удивительно, но если вы посчитаете эти спирали, ваша сумма будет числом Фибоначчи. Разделите спирали на заостренные влево и вправо, и вы получите два последовательных числа Фибоначчи.
Таким образом вы можете расшифровать спиральные узоры в сосновых шишках, ананасах и цветной капусте, которые также отражают последовательность Фибоначчи.
Цветы и ветки
Некоторые растения выражают последовательность Фибоначчи в своих точках роста, местах, где формируются или расщепляются ветви деревьев. Один ствол растет до тех пор, пока не даст ветвь, в результате чего появятся две точки роста. Затем основной ствол дает еще одну ветвь, в результате чего появляются три точки роста. Затем ствол и первая ветвь производят еще две точки роста, доводя общее количество до пяти. Этот паттерн продолжается, следуя числам Фибоначчи.
Кроме того, если вы посчитаете количество лепестков на цветке, вы часто обнаружите, что общее количество является одним из чисел в последовательности Фибоначчи. Например, у лилий и ирисов три лепестка, у лютиков и шиповника пять, у дельфиниумов восемь лепестков и так далее.
Пчёлы
Пчелиная семья состоит из матки, нескольких трутней и множества рабочих. У пчел-самок (маток и рабочих) есть два родителя: трутень и матка. Трутни же вылупляются из неоплодотворенных яиц. Это означает, что у них есть только один родитель. Таким образом, числа Фибоначчи выражают генеалогическое древо дрона в том смысле, что у него есть один родитель, два дедушки и бабушки, три прадедушки и так далее.
Штормы
Штормовые системы, такие как ураганы и торнадо, часто следуют последовательности Фибоначчи. В следующий раз, когда вы увидите на метеорологическом радаре ураган, вращающийся по спирали, обратите внимание на безошибочно узнаваемую спираль Фибоначчи в облаках на экране.
Человеческое тело
Внимательно посмотрите на себя в зеркало. Вы заметите, что большинство частей вашего тела расположены под номерами один, два, три и пять. У вас один нос, два глаза, по три сегмента на каждой конечности и по пять пальцев на каждой руке. Пропорции и размеры человеческого тела также можно разделить по золотому сечению. Молекулы ДНК следуют этой последовательности, имея длину 34 ангстрема и ширину 21 ангстрем для каждого полного цикла двойной спирали.
Почему так много природных закономерностей отражают последовательность Фибоначчи?
Ученые веками размышляли над этим вопросом. В некоторых случаях корреляция может быть просто совпадением. В других ситуациях соотношение существует, потому что эта конкретная модель роста развилась как наиболее эффективная. У растений это может означать максимальное воздействие на светолюбивые листья или максимальное расположение семян.
Заблуждения о золотом сечении
Хотя эксперты согласны с тем, что последовательность Фибоначчи распространена в природе, меньше согласия относительно того, выражается ли последовательность Фибоначчи в определенных случаях искусства и архитектуры. Хотя в некоторых книгах говорится, что Великая пирамида и Парфенон (а также некоторые картины Леонардо да Винчи) были спроектированы с использованием золотого сечения, при проверке это оказалось неверным.
Математик Джордж Марковски указал, что и Парфенон, и Великая пирамида имеют части, которые не соответствуют золотому сечению, что-то упущенное людьми, решившими доказать, что числа Фибоначчи существуют во всем. Термин «золотая середина» использовался в древние времена для обозначения чего-то, что избегало доступа в любом направлении, и некоторые люди объединили золотую середину с золотым сечением, которое является более поздним термином, появившимся в 19 веке.
Интересно
Мы отмечаем День Фибоначчи 23 ноября не только в честь забытого математического гения Леонардо Фибоначчи, но и потому, что когда дата записывается как 23 ноября, четыре числа образуют последовательность Фибоначчи. Леонардо Фибоначчи также часто приписывают вклад в переход от римских цифр к арабским цифрам, которые мы используем сегодня.
Часто задаваемые вопросы
Что такое последовательность Фибоначчи?
Последовательность Фибоначчи представляет собой ряд чисел, в котором каждое число является суммой двух предыдущих чисел. Простейшая последовательность Фибоначчи начинается с 0, 1, 1, 2, 3, 5, 8, 13, 21 и так далее.
