
Самым известным из всех фракталов является множество Мандельброта. Математик Бенуа Мандельброт ввел термин «фрактал» в 1975 году, чтобы назвать новую категорию математики, которая количественно определяет геометрические неровности и порядок внутри кажущихся хаотичными форм.
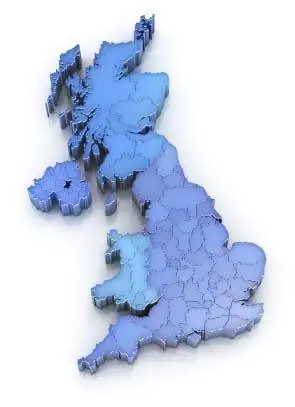
Задолго до того, как Мандельброт дал название фрактальной геометрии, математики бились над концепциями, связанными с фрактальной размерностью. Изучая побережье Англии в первой половине 20 века, Льюис Фрай Ричардсон понял, что чем меньше линейка, тем длиннее будет измерение береговой линии. По мере того, как ваш измерительный инструмент уменьшается, он может захватывать больше деталей контура неровной формы. С точки зрения фракталов, береговая линия Англии бесконечна.

Губка Менгера была разработана Карлом Менгером при изучении количественной оценки топологической размерности. Это может быть менее художественно захватывающим, чем большинство изображений наборов Мандельброта и Джулии, но использование формулы губки Менгера продвинуло многие области науки.

Природа наполнена фрактальными формами. Этот лист папоротника демонстрирует одну из ключевых характеристик фракталов: самоподобие. Каждый крошечный листочек сворачивается в форму, имитирующую большую ветвь.

Ракушки Наутилуса - пример того, как Мать-Природа демонстрирует свои геометрические способности. Каждая камера представляет собой меньшую итерацию предыдущей; в формулах фрактальной геометрии эта характеристика представлена в виде петли обратной связи, где результат одной итерации формулы становится переменной для следующей итерации.

Съешь свою геометрию! Брокколи по-римски растет по такому структурированному повторяющемуся шаблону, что вы можете склониться к мысли, что это было сконструировано злыми учеными, стремящимися к господству над овощами. Неа! Природа позаботится обо всей математике.

Внимательно присмотревшись к снежинке, вы увидите, что черты каждой ветви ее формы выглядят так же, как и снежинка в целом (по крайней мере, пока она не растает). Поиск и количественная оценка этих упорядоченных структур внутри того, что изначально кажется случайным, является одной из основных задач фрактальной геометрии.

Это НЕ увеличенная снежинка; это фрактальное уравнение, представленное визуально. Сходство между естественными фракталами и фракталами, созданными математически, иллюстрирует тесную связь между ними в этой области геометрии.

В то время как природа предлагает бесчисленные примеры фрактальной красоты, как только фрактальные формулы были выражены визуально, путем нанесения их значений на плоскость комплексных чисел, родился новый жанр искусства.

Математику Гастону Джулии приписывают разработку концепции петли обратной связи, используемой во фрактальной геометрии. Его работа в начале 1900-х была ограничена отсутствием компьютера для выполнения вычислений по его формуле, набору Жюлиа. Сегодня цифровые художники используют вариации набора Джулии для создания произведений искусства, подобных этому. Представьте, что Джулия сделала бы с вычислительной мощностью 21 века!

Изменяя переменные в уравнении фрактала, вы можете создавать бесконечные вариации на тему. Если вы внимательно посмотрите на это изображение, вы увидите все меньшие и меньшие итерации множества Мандельброта.

Глядя на визуальные представления фрактальных уравнений, вы начинаете замечать, насколько естественным выглядит весь этот «хаос». Синий цвет этого фрактального изображения позволяет легко увидеть его сходство со скалистым побережьем.
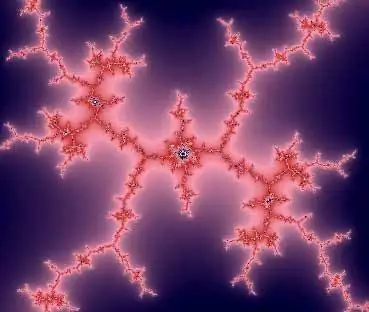
Нарисованные вариации множества Мендельброта часто имеют сегменты усиков, похожих на молнии, и это не совпадение - молния - это естественный фрактал.

Если бы вы увеличили меньшие руки этого рендеринга набора Джулии, вы бы увидели, что они выглядят точно так же, как на большом изображении. Это самоподобие бесконечно проявляется в компьютерных фрактальных моделях, тогда как фракталы, встречающиеся в природе, обычно проходят через ограниченное количество итераций.

Помните те стереограммы со скрытыми изображениями, которые были так популярны в 1990-х? Если вы смотрите на то, что кажется повторяющимся узором, в конечном итоге должно стать видно трехмерное изображение. Некоторые создатели этих произведений искусства используют фракталы в качестве основы для своих фонов. Это изображение выглядит так, как будто оно стереографическое, но на самом деле это обычный фрактал.

Наконец, пример того, как фрактальная геометрия может быть красивой и практичной. Этот экспонат под открытым небом был построен с использованием фракталов для создания теплорассеивающего зонта в Токио. Углы, созданные с помощью фрактальных тетраэдров, рассеивают тепло более эффективно, чем тень с плоской крышей. Узнайте больше о том, как работают фракталы.
