
Вы когда-нибудь задумывались, как компьютер может делать что-то вроде баланса чековой книжки, или играть в шахматы, или проверять орфографию в документе? Это вещи, которые всего несколько десятилетий назад могли делать только люди. Теперь компьютеры делают это с кажущейся легкостью. Как «чип», состоящий из кремния и проводов, может делать то, что, казалось бы, требует человеческого мышления?
Если вы хотите понять ответ на этот вопрос в самой основе, первое, что вам нужно понять, это то, что называетсяБулевая логика Булева логика, первоначально разработанная Джорджем Boole в середине 1800-х годов позволяет отображать довольно много неожиданных вещей в биты и байты. Самое замечательное в булевой логике то, что, как только вы во всем разберетесь, булевская логика (или, по крайней мере, ее части, необходимые для понимания работы компьютеров) станет невероятно простой. В этой статье мы сначала обсудим простые логические «гейты», а затем посмотрим, как их объединить во что-то полезное.
Простые ворота
Есть три, пять или семь простых ворот, о которых вам нужно узнать, в зависимости от того, как вы хотите их считать (сейчас вы поймете, почему). С помощью этих простых вентилей вы можете создавать комбинации, которые реализуют любой цифровой компонент, который вы только можете себе представить. Здесь эти ворота кажутся суховатыми и невероятно простыми, но в следующих разделах мы увидим несколько интересных комбинаций, которые сделают их намного более вдохновляющими. Если вы еще этого не сделали, перед продолжением будет полезно прочитать «Как работают биты и байты».
НЕ Ворота
Простейший возможный вентиль называется "инвертором" или вентилем НЕ. Он принимает на вход один бит и выдает на выходе его противоположность. Логическая таблица:
Вопрос
0 1
1 0
Гейт НЕ имеет один вход с именемAи один выход с именемQ (" Q" используется для выхода, потому что если вы использовали «О», вы легко спутаете его с нулем). В таблице показано, как ведут себя ворота. Когда вы применяете 0 к A, Q дает 1. Когда вы применяете 1 к A, Q дает 0. Просто.
Ворота И
Элемент И выполняет логическую операцию «И» на двух входах, A и B:
A B Q
0 0 0
0 1 0
1 0 0
1 1 1
Идея логического элемента AND заключается в следующем: «Если AAND B равны 1, то Q должен быть равен 1». Вы можете увидеть это поведение в логической таблице для вентиля. Вы читаете эту таблицу построчно, вот так:
A B Q
0 0 0 Если A равно 0 И B равно 0, Q равно 0.
0 1 0 Если A равно 0 И B равно 1, Q равно 0.
1 0 0 Если A равно 1 И B равно 0, Q равно 0.
1 1 1 Если A равно 1 И B равно 1, Q равно 1.
Ворота ИЛИ
Следующие ворота являются воротами ИЛИ. Его основная идея такова: «Если A равно 1OR B равно 1 (или оба равны 1), то Q равно 1».
A B Q
0 0 0
0 1 1
1 0 1
1 1 1
Это три основных врата (это один из способов их подсчета). Довольно часто также распознаются два других:NANDиNOR. Эти два вентиля представляют собой просто комбинации вентилей И или ИЛИ с вентилем НЕ. Если включить эти двое ворот, то счет возрастет до пяти. Вот основная работа вентилей И-НЕ и ИЛИ-НЕ - вы можете видеть, что это просто инверсии вентилей И и ИЛИ:
Врата НОР
A B Q
0 0 1
0 1 0
1 0 0
1 1 0
Врата И-НЕ
A B Q
0 0 1
0 1 1
1 0 1
1 1 0
Последние два входа, которые иногда добавляются в список, - этоXORиXNOR, также известные как «исключающее ИЛИ». и «исключительные ни» ворота соответственно. Вот их таблицы:
Врата XOR
A B Q
0 0 0
0 1 1
1 0 1
1 1 0
Врата XNOR
A B Q
0 0 1
0 1 0
1 0 0
1 1 1
Идея ворот XOR заключается в следующем: «Если либо AORB равно 1, ноНЕ оба, Q равно 1. "Причина, по которой XOR не может быть включена в список вентилей, заключается в том, что вы можете легко реализовать его, используя исходные три перечисленных вентиля.
Если вы попробуете все четыре различных шаблона для A и B и проследите их по схеме, вы обнаружите, что Q ведет себя как вентиль XOR. Поскольку для логических элементов XOR существует хорошо понятный символ, обычно проще думать о XOR как о «стандартном вентиле» и использовать его так же, как AND и OR на принципиальных схемах.
Простые сумматоры
В статье о битах и байтах вы узнали одвоичном сложении. В этом разделе вы узнаете, как создать схему, способную к двоичному сложению, используя элементы, описанные в предыдущем разделе.
Начнем содноразрядного сумматораДопустим, у вас есть проект, в котором вам нужно сложить отдельные биты вместе и получить ответ. Чтобы начать разработку схемы для этого, сначала посмотрите на все логические комбинации. Вы можете сделать это, взглянув на следующие четыре суммы:
0 + 0=0
0 + 1=1
1 + 0=1
1 + 1=10
Это выглядит нормально, пока вы не дойдете до 1 + 1. В этом случае вам придется беспокоиться об этом надоедливомбите переноса. Если вас не волнует перенос (потому что это, в конце концов, проблема сложения 1 бита), то вы можете увидеть, что можете решить эту проблему с помощью вентиля XOR. Но если вам не все равно, вы можете переписать свои уравнения так, чтобы они всегда включали2 бита вывода, например:
0 + 0=00
0 + 1=01
1 + 0=01
1 + 1=10
Из этих уравнений можно составить логическую таблицу:
1-битный сумматор с переносом
A B Q CO
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1
Глядя на эту таблицу, вы можете видеть, что вы можете реализовать Q с вентилем XOR и CO (выполнение) с вентилем AND. Просто.
Что делать, если вы хотите сложить вместе два 8-битных байта? Это становится немного сложнее. Самое простое решение - разделить проблему накомпоненты многократного использования, а затем реплицировать компоненты. В этом случае нам нужно создать только один компонент:полный двоичный сумматор.
Разница между полным сумматором и предыдущим сумматором, который мы рассмотрели, заключается в том, что полный сумматор принимает входные данные A и B, а также вводпереноса (CI). Когда у нас есть полный сумматор, мы можем соединить восемь из них вместе, чтобы создать сумматор шириной в байт и каскадировать бит переноса от одного сумматора к другому.
В следующем разделе мы рассмотрим, как полный сумматор реализуется в схеме.
Полные сумматоры
Логическая таблица для полного сумматора немного сложнее, чем таблицы, которые мы использовали ранее, потому что теперь у нас есть3 входных бита. Выглядит это так:
Однобитовый полный сумматор с переносом и переносом
CI A B Q CO
0 0 0 0 0
0 0 1 1 0
0 1 0 1 0
0 1 1 0 1
1 0 0 1 0
1 0 1 0 1
1 1 0 0 1
1 1 1 1 1
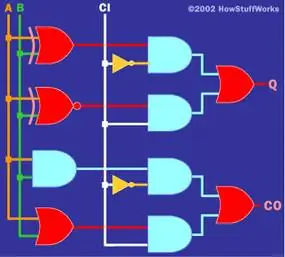
Эту таблицу можно реализовать разными способами. Я собираюсь представить здесь один метод, преимущество которого заключается в простоте понимания. Если вы посмотрите на бит Q, вы увидите, что верхние 4 бита ведут себя как вентиль XOR по отношению к A и B, а нижние 4 бита ведут себя как вентиль XNOR по отношению к A и B. Точно так же верхние 4 бита CO ведут себя как вентиль И по отношению к A и B, а нижние 4 бита ведут себя как вентиль ИЛИ. Учитывая эти факты, следующая схема реализует полный сумматор:
Это определенно не самый эффективный способ реализации полного сумматора, но его чрезвычайно легко понять и проследить логику, используя этот метод. Если вы так склонны, посмотрите, что вы можете сделать, чтобы реализовать эту логику с меньшим количеством ворот.
Теперь у нас есть часть функциональности, которая называется "полный сумматор". Что тогда делает компьютерный инженер, так это «черный ящик», чтобы он или она могли перестать беспокоиться о деталях компонента.черный ящик для полного сумматора будет выглядеть так:

С этим черным ящиком теперь легко нарисовать4-битный полный сумматор:
На этой диаграмме перенос каждого бита подается непосредственно на перенос следующего бита. 0 жестко зашит в начальный бит переноса. Если вы введете два 4-битных числа в строки A и B, вы получите 4-битную сумму в линиях Q плюс 1 дополнительный бит для окончательного переноса. Вы можете видеть, что эта цепочка может расширяться как угодно, через 8, 16 или 32 бита, если это необходимо.
Только что созданный нами 4-битный сумматор называетсясумматор с переносом пульсаций. Он получил такое название, потому что биты переноса «колеблются» от одного сумматора к другому. Преимуществом этой реализации является простота, но недостатком являются проблемы со скоростью. В реальной схеме вентилям требуется время для переключения состояний (время порядка наносекунд, но в высокоскоростных компьютерах важны наносекунды). Таким образом, 32-битным или 64-битным сумматорам с переносом пульсаций может потребоваться от 100 до 200 наносекунд, чтобы установить окончательную сумму из-за пульсаций переноса. По этой причине инженеры создали более продвинутые сумматоры, называемые сумматорамиcarry-lookahead. Количество вентилей, необходимых для реализации упреждающего переноса, велико, но время установки сумматора намного лучше.
Вьетнамки

Одна из наиболее интересных вещей, которые вы можете делать с логическими воротами, - это создавать с их помощьюпамять. Если вы правильно расположите ворота, они запомнят входное значение. Эта простая концепция лежит в основе ОЗУ (оперативной памяти) в компьютерах, а также позволяет создавать множество других полезных схем.
Память опирается на понятиеобратная связь. То есть выход вентиля подается обратно на вход. Простейшая возможная схема обратной связи с использованием двух инверторов показана выше.
Если вы проследите путь обратной связи, вы увидите, что если Q равно 1, оно всегда будет 1. Если оно равно 0, оно всегда будет 0. Так как приятно иметь возможность контролировать схемы, которые мы создаем, эта не очень полезна, но позволяет увидеть, как работает обратная связь.
Оказывается, что в «реальных» схемах вы действительно можете использовать такой простой подход обратной связи инвертора. Более полезнаясхема обратной связи, использующая два вентиля И-НЕ, показана ниже:
Эта схема имеет два входа (RиS) и два выхода (Q). иQ'). Из-за обратной связи его логическая таблица немного необычна по сравнению с теми, что мы видели ранее:
R S Q Q'
0 0 Незаконно
0 1 1 0
1 0 0 1
1 1 помнит
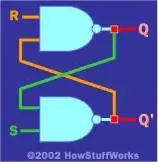
Логическая таблица показывает следующее:
- Если R и S противоположны друг другу, то Q следует за S, а Q' является инверсией Q.
- Если оба R и S переключены в 1 одновременно, то схемазапоминает то, что ранее было представлено на R и S.
Есть также смешноенелегальноегосударство. В этом состоянии R и S оба переходят в 0, что не имеет значения в смысле памяти. Из-за недопустимого состояния вы обычно добавляете небольшуюлогику кондиционированияна стороне ввода, чтобы предотвратить это,s, показанные здесь:
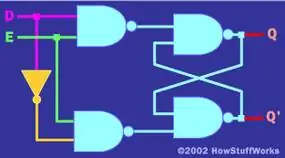
В этой схеме есть два входа (D и E). Вы можете представитьDкак «Данные», аEкак «Включить». Если E равно 1, то Q будет следовать за D. Однако, если E изменится на 0, Q запомнит то, что в последний раз видели на D. Схема, которая ведет себя таким образом, обычно называетсятриггером.
В следующем разделе мы рассмотрим триггер JK.
JK Flip-Flop
Очень распространенной формой триггера являетсяJK flip-flop. Исторически неясно, откуда взялось имя «JK», но обычно оно представлено в черном ящике, например:
На этой диаграммеPозначает «Preset»,Cозначает «Clear» иClkозначает «Часы».
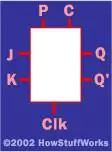
P C Clk J K Q Q'
1 1 1-to-0 1 0 1 0
1 1 1-to-0 0 1 0 1
1 1 1-to-0 1 1 Переключение
1 0 x x x 0 1
0 1 x x x 1 0
Вот что написано в таблице: Во-первых, Preset и Clear полностью переопределяют J, K и Clk. Таким образом, если Preset становится равным 0, то Q становится равным 1; и если Clear становится равным 0, то Q становится равным 0 независимо от того, что делают J, K и Clk. Однако, если и Preset, и Clear равны 1, то J, K и Clk могут работать. Обозначение1-to-0означает, что когда часы меняются с 1 на 0, значения J и K запоминаются, если они противоположны. Нанижнем фронтечасов (переход от 1 к 0) сохраняются J и K. Однако, если и J, и K равны 1 на низком фронте, то Q простопереключается То есть Q переходит из своего текущего состояния в противоположное состояние.
Возможно, прямо сейчас вы спрашиваете себя: «Для чего это нужно?» Оказывается, концепция «срабатывания по фронту» очень полезна. Тот факт, что триггер JK только «защелкивает» входы JK только при переходе от 1 к 0, делает его гораздо более полезным в качестве запоминающего устройства. Триггеры JK также чрезвычайно полезны всчетчиках(которые широко используются при создании цифровых часов). Вот пример4-битного счетчика с использованием JK-триггеров:
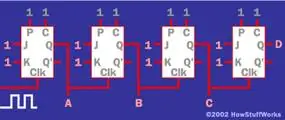
Выходами этой схемы являются A, B, C и D, и они представляют собой 4-битное двоичное число. На тактовый вход крайнего левого триггера поступает сигнал, многократно изменяющийся от 1 до 0 и обратно до 1 (осциллирующий сигнал). Счетчик будет подсчитывать низкие фронты, которые он видит в этом сигнале. То есть каждый раз, когда входящий сигнал изменяется с 1 на 0, 4-битное число, представленное A, B, C и D, будет увеличиваться на 1. Таким образом, счет будет идти от 0 до 15, а затем циклически возвращается к 0. Вы можете добавлять к этому счетчику столько битов, сколько хотите, и считать все, что угодно. Например, если вы поместите магнитный переключатель на дверь, счетчик будет подсчитывать, сколько раз дверь открывалась и закрывалась. Если вы поместите оптический датчик на дорогу, счетчик сможет подсчитать количество проезжающих машин.
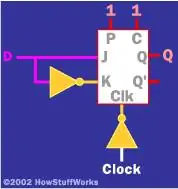
Другое использование JK-триггера - созданиезащелки, запускаемой фронтом, как показано здесь.
В этом случае значение на D "фиксируется", когда фронт тактового сигнала переходит от низкого к высокому. Защелки чрезвычайно важны при разработке таких вещей, как центральные процессоры (ЦП) и периферийные устройства в компьютерах.
Реализация ворот
В предыдущих разделах мы видели, что, используя очень простые логические элементы, мы можем реализовывать сумматоры, счетчики, защелки и так далее. Это большое достижение, потому что не так давно люди были единственными, кто мог делать такие вещи, как сложение двух чисел. Приложив немного усилий, можно спроектировать булевы схемы, реализующие вычитание, умножение и деление. Вы можете видеть, что мы не так уж далеко ушли от карманного калькулятора. Отсюда недалеко до полноценных процессоров, используемых в компьютерах.
Итак, как мы можем реализовать эти ворота в реальной жизни? Мистер Буль придумал их на бумаге, и на бумаге они прекрасно смотрятся. Однако, чтобы их использовать, нам нужно реализовать их в физической реальности, чтобы ворота могли активно выполнять свою логику. Как только мы совершим этот скачок, мы вступим на путь создания настоящих вычислительных устройств.
Самый простой способ понять физическую реализацию булевой логики - использовать реле. Собственно, так и были реализованы самые первые компьютеры. Никто больше не реализует компьютеры с реле - сегодня люди используют субмикроскопические транзисторы, выгравированные на кремниевых чипах. Эти транзисторы невероятно маленькие и быстрые, и они потребляют очень мало энергии по сравнению с реле. Однако реле невероятно просты для понимания, и они могут очень просто реализовывать булеву логику. Из-за этой простоты вы сможете увидеть, что отображение «ворот на бумаге» в «активные ворота, реализованные в физической реальности» возможно и просто. Выполнить такое же сопоставление с транзисторами так же просто.
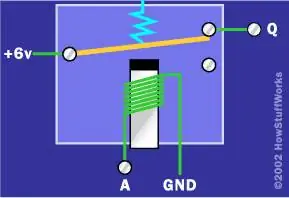
Начнем с инвертора. Реализовать логический элемент НЕ с помощью реле очень просто: мы собираемся использовать напряжения для представления битовых состояний. Мы определим двоичную 1 как 6 вольт, а двоичный 0 как ноль вольт (земля). Затем мы будем использовать 6-вольтовую батарею для питания наших схем. Таким образом, наш вентиль НЕ будет выглядеть так:
[Если эта цифра не имеет для вас никакого смысла, прочтите, как работают реле, чтобы получить объяснение.]
Вы можете видеть в этой схеме, что если вы приложите ноль вольт к A, то вы получите 6 вольт на выходе Q; и если вы приложите 6 вольт к A, вы получите 0 вольт на выходе Q. Очень легко реализовать инвертор с реле!
Так же легко реализовать вентиль И с двумя реле:
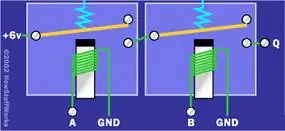
Здесь видно, что если подать 6 вольт на A и B, на Q будет 6 вольт. В противном случае Q будет иметь ноль вольт. Это именно то поведение, которое мы хотим от вентиля И. Ворота ИЛИ еще проще - просто соедините два провода для A и B вместе, чтобы создать ИЛИ. Вы можете пойти дальше и использовать два реле параллельно.
Из этого обсуждения видно, что вы можете создать три основных элемента - НЕ, И и ИЛИ - из реле. Затем вы можете соединить эти физические вентили вместе, используя логические схемы, показанные выше, чтобы создать физический 8-битный сумматор с пульсирующим переносом. Если вы используете простые переключатели для подачи входов A и B на сумматор и подключите все восемь линий Q к лампочкам, вы сможете сложить любые два числа и прочитать результаты на лампочках («свет горит»=1, « свет выключен"=0).
Булевая логика в виде простых вентилей очень проста. Из простых вентилей можно создавать более сложные функции, например сложение. Физически реализовать ворота возможно и просто. Из этих трех фактов у вас есть сердце цифровой революции, и вы понимаете, как работают компьютеры.
